J.S.Bach

"mathe kontra physik"
upd. 22. Nov. 2001

Berechnung der Frequenzen
Anmerkung:
Da die Berechnung (Tabellenkalkulation) mit einer MS-Excel-Tabelle durchgeführt werden soll, sind die Formeln in MS-Excel Schreibweise angegeben.

Da die nächst höhere Oktave die doppelte und nächst niedrigere Oktave die halbe Frequenz haben muss und alle Halbtone-Schritte bei der Wohltemperierten Stimmung "gleichberechtigt" sein sollen, ergibt sich für den nächst höheren Halbton

= A1 * POTENZ(2,1/2)

Erläuterung zur Excel-Schreibweise:
Die betrachtete Frequenz steht in Zelle A1.
POTENZ(2,1/2) bedeutet "12. Wurzel aus 2".

Warum "12. Wurzel aus 2"?
Antwort:
(12. Wurzel aus 2) hoch 12 ergibt 2, also die doppelte Frequenz, die Oktave.

Aufgabe 2
Berechnen Sie mit Hilfe einer Kalkulationstabelle alle Töne - incl. Halbtöne - einer Tonleiter.

Berechnung der Schwebungsfrequenzen




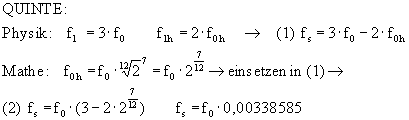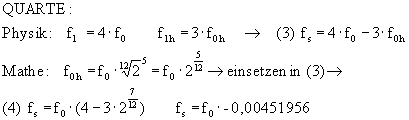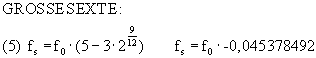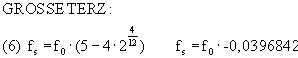Eine negative Schwebungsfrequenz bedeutet dabei, dass der Intervall gegenüber der physikalischen Reinheit vergrössert werden muss, während eine positive Schwebungsfrquenz bedeutet, dass der Intervall gegenüber der physikalischen Reinheit verkleinert werden muss.

In der Excel-Schreibweise kann man entsprechend mit
fs = Schwebungsfrequenz und f0 = Frequenz des tiefen Tones
schreiben:

Ton-Intervall MS-Excel-Ausdruck für fs Ergebnis
Quinte =f0 * ( 3-2*POTENZ(2;7/12) ) positiv => kleiner
Quarte =f0 * ( 4-3*POTENZ(2;5/12) ) negativ => größer
grosse Sexte =f0 * ( 5-3*POTENZ(2;9/12) ) negativ => größer
grosse Terz =f0 * ( 5-4*POTENZ(2;1/3) ) negativ => größer


Aufgabe 3
Berechnen Sie mit Hilfe einer Kalkulationstabelle (und der Lösungen von Aufgabe 2) die erforderliche Schwebungsfrequenz von a1 (440 Hz) zu d1 (Quinte nach unten).

Aufgabe 4
Schreiben Sie die obige Ableitung für "Quinte" in der mathematischen Schreibweise nach.
Hinweis: MS-Word, Einfügen, Objekt, Formel-Editor (muss installiert sein)

zurück   weiter