 J.S.Bach
J.S.Bach |
"wohltemperiert"
|
22. Nov. 2001 |
|
Was bedeutet "wohltemperiert" ?
Man kann bei der Wohltemperierten Stimmung ("Erfinder" Andreas
Werckmeister) von Tasteninstrumenten auf jeder der 12 Tasten einer
Oktave je eine Dur- und eine Molltonleiter beginnen - ohne störend
falsch klingende Intervalle wie bei anderen, älteren Stimmungen.
So ergeben sich in Bachs Wohltemperiertem Klavier 2 mal 24 für
Präludien und Fugen.
Bei der Wohltemperierte Stimmung muss man die Intervalle "zur Gleichberechtigung"
abweichend von der "Physik" leicht verstimmen und zwar "mathematisch"
exakt.
Früher existierten noch andere Stimmungen, die zwar sehr gut in
wenigen Tonarten klangen, aber "grausam" in weiteren Tonarten
(siehe Auseinandersetzung Bachs mit Orgelbauer Silbermann und
Wolfsquinte).
Selbstverständlich kann man Berechnungen für diese "alten
Stimmungen" auch gut mit Kalkulationstabellen durchführen.
Siehe unten mit MS-Excel.
Frequenzen, Schwebungen, Berechnungen
Während die meisten Menschen - abgesehen von denen mit einem
absoluten Gehör - die Höhe (Frequenz) eines einzelnen
Tones nicht genau angeben können, lässt sich das Stimmen von
Instrumenten auf Grundlage der erforderlichen Schwebungen erlernen.
Schwebungen lassen sich besonders gut hören, wenn zwei Töne
zusammenklingen, die in ihrer Grundfrequenz nur sehr wenig abweichen.
Da Töne aus einem Frequenzspektrum bestehen, also selbst noch mehrere
Obertöne haben, lassen sich auch Schwebungen zwischen diesen Partialtönen
zweier Töne gut wahrnehmen. Partialtöne bilden sind "physikalisch
rein". Sie haben Vielfachfache der Grundfrequenz.
Wenn man auf einem Tasteninstrument entsprechend dieser "Physik"
12 Quinten hintereinander (in einer Richtung) rein stimmen würde
- wobei man wieder auf den gleichnamen Ton trifft -, dann weicht dieser
Ton sehr hörbar vom Grundton ab. Er ist zu hoch. Das wusste schon
der alte Pythagoras (Pythagoräisches Komma). Alle Quinten
sind also "zu gross". Beim Stimmen werden sie quasi "passend
verkleinert".
Die Berechnungen, die der Tabelle unten zugrunde liegen ("Mathematik
kontra Physik") befinden sich [
hier ].
Wie stimmt man also ?
Im Folgenden ist eine Kalkulationstabelle dargestellt mit der Stimm-Vorgehensweise
"Kleine Temperatur", die man in der angegebenen oder der nächst
höheren Oktave ausführen kann. Das geschieht in 11 Schritten
(schwarze Pfeile) mit verschiedenen eingeschobenen Prüfschritten
(blaue Strecken). Vorausgesetzt werden 440 Hz für den Kammerton.
Selbstverständlich kann man in einer Kalkulationstabelle (hier
MS-Excel, download als zip-Datei) auch eine andere Kammertonfrequenz
wählen, wobei sofort die richtigen Werte erscheinen.
Bei den einzelnen Stimm-Schritten müssen die errechneten Schwebungen
ausgezählt werden. Da man nicht "2,5 Schwebungen je Sekunde"
zählen kann, zählt man z.B. die Schwebungen innerhalb von
10 Sekunden.
Legende für die Tabelle:
5 => Quinte - muss gegenüber einer reinen Stimmung verkleinert
werden (schwarze Zahlen)
4 => Quarte - muss gegenüber einer reinen Stimmung vergrössert
werden (rote Zahlen)
3+ => grosse Terz - muss gegenüber einer reinen Stimmung vergrössert
werden (rote Zahlen)
6+ => grosse Sexte - muss gegenüber einer reinen Stimmung vergrössert
werden (rote Zahlen)
Pfeil-Folge => Vorgehen beim Stimmen
blaue Strecken => Kontroll-Intervalle
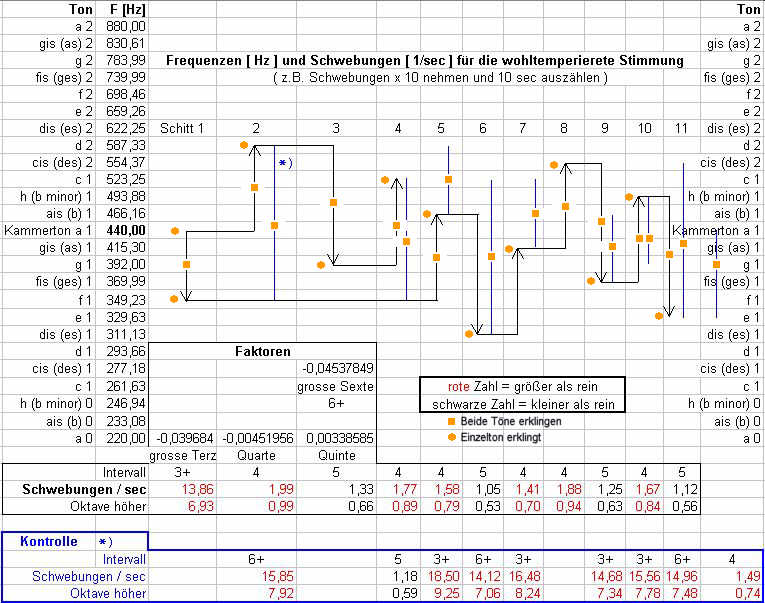
Sie können auch einen Computer mit Sound-Wiedergabe neben das zu
stimmende Gerät stellen und sich die gewünschten Töne
durch Klick auf die Markierungen im Bild oben (Kreise in organe) vorspielen,
was allerdings nur gilt, wenn Sie den Kammerton bei 440 Hertz haben
wollen. Klavier und Orgelstimmer geben allerdings an, dass sie mit der
Schwebungsmethode schneller, genauer und sicherer stimmen.
Die mathematisch-physikalischen Grundlagen
für obige Tabelle finden Sie [ hier
].
Aufgabe 1
Kann obige Tabellenkalkulation auch für andere Kammertonfrequenzen
benutzt werden? Wie?